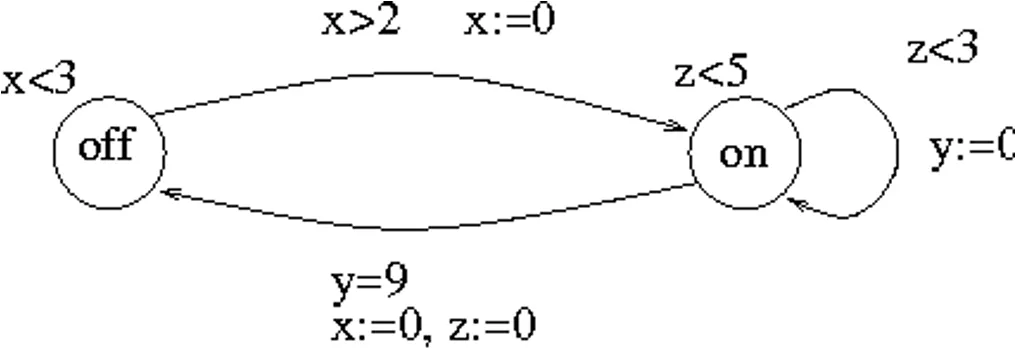课程信息
Finite Automata
- 自动机定义:
- 有限个states(Q)
- 一个输入字母表(Σ)
- 一个转移函数(δ) δ(q,a)
- 开始状态(q0∈Q)
- 结束状态集合(F)
- (Q,Σ,δ,q0,F)
- 转移表
- ...w,x,y,z通常表示字符串,a,b,c,...表示单个输入符号
- 拓展δ:δ(q,wa)=δ(δ(q,w),a)
- L(A)是自动机A的语言
- 如何证明自动机的描述性语言和自动机的表示语言相同:对于字符串长度进行归纳
- 如果L和某个DFA接受的语言相等那称为regular正则
- 正则语言不能数数,不是正则的反例{0n1n∣n≥1}
- 反证法,若存在这样的DFA有m个状态,能够接受0m1m,那么对于前m个字符,必须要有m+1个状态,鸽笼原理可得有一个重复,则能够接受0m′1m
- 同理,{w∣w是平衡的括号序列}也不是
- 但{w∣w能被23整除}是
- 不确定性自动机
- 同DFA,只是δ的结果是一个集合
- NFA−>DFA: 子集构造法
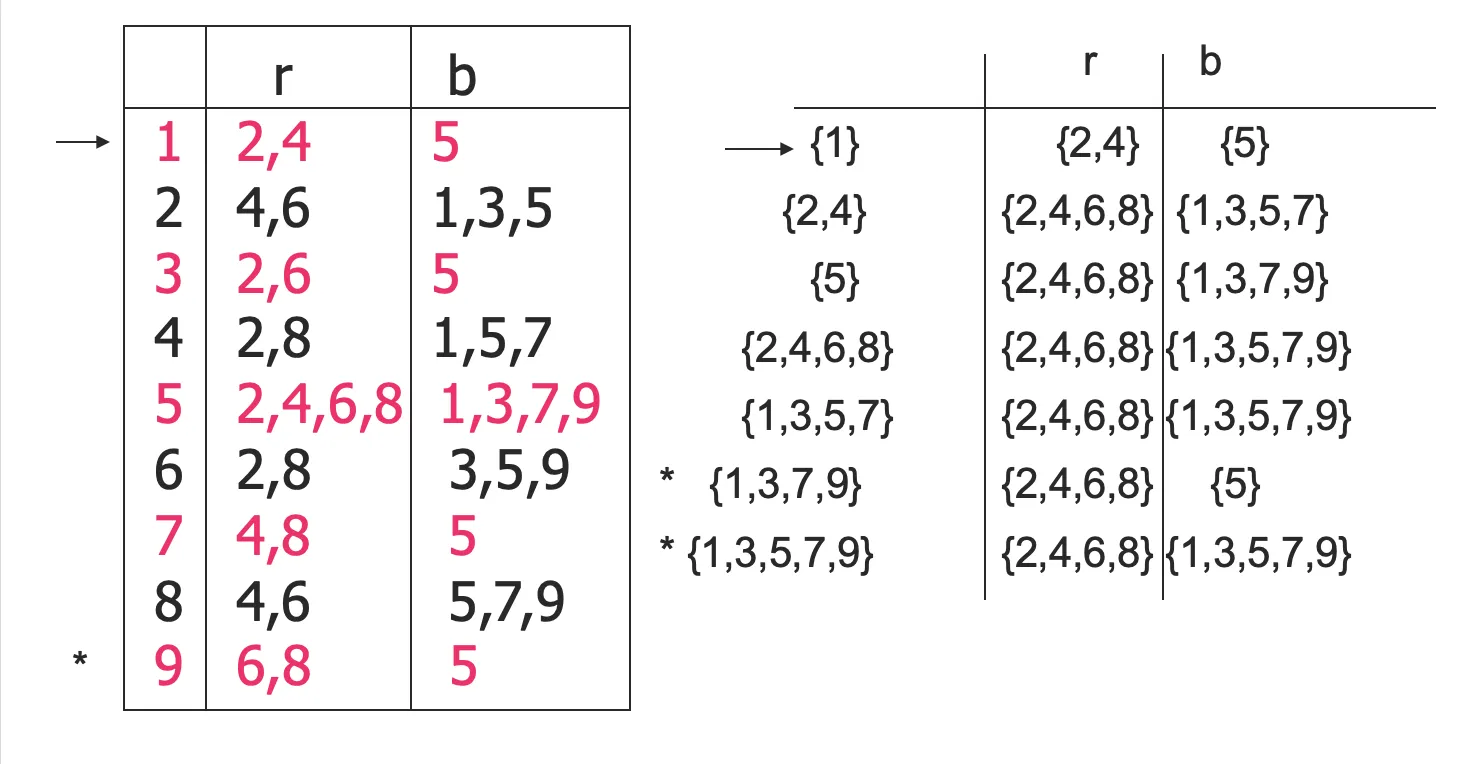
- ϵ−NFA−>NFA
- 设原来的转移函数是δE,新转移函数δN
- δN(q,a)=∪p∈CL(q)δE(p,a)
- F′={q∣CL(q)∧F=∅}
Regular Expression
- *优先级最高,其次是连接,最后是+
- RE->NFA (对于每个表达式构造ϵ−NFA)
- DFA->RE:
- 对于DFA上的状态进行编号,1...n
- k-PATH: 任意经过的状态编号都<=k,但起点和终点不受限制
- 对于k-PATH的k进行归纳,证明路径可以被正则表达式表达
- 判定性质:
- Membership(直接模拟)
- Emptiness从开始状态找是否有可到达的结束状态
- Infiniteness语言是否无限?
- 如果DFA有n个状态,如果语言含有长度>=n的字符串,那语言无限(鸽巢原理)
- 如果语言有[n,2n−1]长度的字符串,那语言无限(鸽巢原理)
- 仍然效率感人,所以不如在消除死状态后判断是否有环
- 崩引理:对于每个正则语言L,存在一个整数n,对于每个w∈L长度大于等于n, 可以写出w=xyz,使得:
- ∣xy∣≤n
- ∣y∣>0
- xyiz∈L,i≥0
- 继续判定性质:
- Equivalence, 两个语言是否相等?构造乘积自动机,两个都是final states就接受
- Containment,两个语言是否包含?构造乘积自动机,[q,r]中q是A的接受状态,r不是B的接受状态,如果这个乘积自动机为空说明是子集。
- DFA最小化:
- 画出一个n*n的表格,如果一个状态是接受状态,一个状态不是,那么标记这两个状态是可区分的。
- 继续,对于所有未标记的状态对,如果对于同一个输入到达的两个状态已经被标记可区分了,那么这两个状态也被标记为可区分。
- 最后不能再继续标记的表格中,没有被标记为可区分的可以被合并
- 最小化后可能会出现死状态,得继续消除。
- 证明这样确实是最小的:
- 假设确实有更小的B,则A,B起始状态不可区分(因为接受的字符串相同)
- 根据归纳法,A中每个可达状态都在B中存在一个状态与其不可区分
- 根据鸽巢原理,由于A状态数大于B,则A中有两个状态和B中的同一状态不可区分,传递性发现这两个状态也不可区分,矛盾。
- 正则语言的闭包性质:
- Union(根据正则表达式)
- 拼接和Kleene闭包(同样根据正则表达式)
- Intersection (乘积自动机)
- Difference(乘积自动机)
- Complemention (Σ∗−L)
- Reversal (在正则表达式上直接构造)
- Homomorphism (在正则表达式上直接同态过去得到新表达式)
- 逆同态
- 构造一个新的DFA B,状态集合和A完全一致
- 转移函数δB(q0,w)=δA(q0,h(w))
- 可以对于w进行归纳
Context-Free Language
- Terminals 终结符号,Variables(非终结符号)变量,Start Symbol开始符号,产生式
- 如果A→γ是一个产生式,那么我们说αAβ=>αγβ; =>∗定义
- CFL语言可以数两个东西,但不能数三个
- BNF记号: 变量写在<...>里,多字符的终止符通常用加粗或者下划线表示while或者WHILE,::=通常用于表示->,用[...]表示可选
- 最左推导,最右推导
- Parse Tree;叶子是终结符号或者ϵ
- Parse Tree和最左/最右推导等价
- 对于树高进行归纳
- 如果一个CFG能够推导出两个parse tree,那么其是一个二义性语法
- 对于有些语法,二义性语法是不可避免的,如{0i1j2k∣i=j or j=k}
- CFL语言的化简
- 无用变量(是否有变量不能推导出终结符):从A−>w逐步推导
- 不可到达(是否有产生式不能从开始符号推导出来):从S逐步推导
- 去除Epsilon产生式(当然语言中不能有ϵ)
- 先找到nullable的变量(即A=>∗ϵ)
- 对于每个产生式S−>X1X2X3..Xn对于右边的每个可空变量,都考虑它是空或者不为空的情况(除去全为空,2n−1种)
- 证明对于推导步数进行归纳即可
- 单元产生式A−>B
- 先找到单元对(A,B),即A=>∗B全由单元产生式推导出(从(A,A)开始归纳)
- 对于每个单元对(A,B)找到B的所有非单元产生式B−>α,将A−>α加入语法中
- 删除所有单元产生式
- 清理的时候先消除ϵ产生式,再消除单元产生式,再消除无用变量,最后再消除不可达变量(epsilon表达式消除后可能会产生单元表达式或者无用变量)
- CNF 乔姆斯基范式
- A−>BC或者A−>a
- 先清理文法,使得每个产生式都是只有一个终结符号或者长度>=2
- 对于>=2的产生式,把所有终结符号都用变量代替
- 然后切分成二元产生式,A→BCDE => A→BF,F→..
Pushdown Automata
- PDA被以下定义:
- 有限个状态 (Q)
- 输入字母表 (Σ)
- 栈字母表 (Γ)
- 转移函数 (δ)
- 开始状态 (q0)
- 开始符号 (Z0∈Γ)
- 接受状态 (F)
- 通常a,b,...是输入符号,...X,Y,Z是栈符号,...w,x,y,z是输入符号的字符串,α,β,...是栈符号的字符串
- δ(q,a,Z)=(p,α)
- PDA的状态可以用(q,w,α)描述,q是当前状态,w是剩余输出,α是栈内内容
- ID I, ID j; I可以在PDA一步推导出J, I⊢J
- 定义PDA语言的一种方法是用接受状态,L(P)={w∣(q0,w,Z0)⊢∗(f,ϵ,α))}
- 另一种方法是用空栈,N(P)={w∣(q0,w,Z0)⊢∗(q,ϵ,ϵ))}
- L(P)和N(P)表达能力相同:
- L(P)−>N(P′):P'会模拟P,如果P接受,那么P′会清空栈.在栈底加上一个保护性元素以防栈被其他时刻清空。
- N(P)−>L(P′):P'会模拟P,在栈底用一个保护性元素检测什么时候P清空栈,此时P′接受
- 确定性PDA没有不确定性自动机那么强大: 对于需要猜测的语言,如wwR这样PDA需要猜测回文串的分隔位置,DPDA不能处理。可以为其提供一个决策依据wcwR
- 正则语言一定能被DPDA表达
- DPDA的L(P)和N(P)不相等,因为DPA中的空栈一旦到达,就死机了(确定性原则);如{0n∣n≥0}
- CFG->PDA:
- 只有一个状态q
- 输入符号是CFG的所有终结符号
- 栈符号是CFG的所有符号
- 起始符号是CFG的其实符号
- δ(q,a,a)=(q,ϵ) 把产生式的匹配转移到输入串上
- δ(q,ϵ,A)+=(q,α)对于A−>α 展开产生式
- 通过对PDA移动步数和最左推导进行归纳
- PDA->CFG
- 使用[pXq]代表变量,该变量生成的字符串w,代表PDA从p开始,在读入w后进入状态q,并把栈顶符号X弹出
- δ(p,a,X)包含(q,ϵ),[pXq]→a直接弹出
- δ(p,a,X)包含(r,Y),[pXq]→a[rYq]先读a进入状态r再到达q
- δ(p,a,X)包含(r,YZ),[pXq]→a[rYs][sZq]
- 起始符号S,并对于任何可能的状态p,添加产生式S→[q0Z0p] (空栈可以在任何状态被接受)
CFL&PDA
- 泵引理
- 对于一个CFLL,存在一个整数n,对于每个在L中长度大于等于n的字符串z,存在z=uwvxy使得:
- ∣vwx∣≤n
- ∣vx∣>0
- uviwxiy∈L
- {0i10i10i∣i≥1}
- Decision Properties:
- Emptiness: 消除可空变量
- Membership: CYK算法
- xi,j表示字符串中[i,j]能表示的变量
- Infiniteness: 看看有没有长度在[n,2n−1]之间的字符串,有就无限
- 闭包性质
- Union: 明显闭包
- 拼接:明显闭包
- Star:明显闭包
- 反转: 封闭,把每个产生式都反转
- 同态: 产生式把每个都换成同态后的结果
- 交集: 不闭包
- {0n1n2n∣n≥1}不是CFL,但{0i1n2n∣n≥1}和{0n1n2i}都是,他们的交集是第一个,不是CFL。
- 差: 不闭包
- L∩M=L−(L−M)
- 但是CFL和正则语言的交集仍然是CFL
- 将DFA和PDA并行运行,如果两个都接受才接受(如果遇上ϵ则DFA状态保持不变)
- 逆同态的证明
- 构造PDA P', 接受w当且P接受h(w) 就是在输入端用状态模拟出一个buffer
- 状态是[q,w],q是P的一个状态,w是h(a)的一个suffix
- 开始状态时[q0,ϵ],结束状态是[f,ϵ]
- δ′([q,ϵ],a,X)={([q,h(a)],X)}从输入中获得buffer
- δ′([q,bw],ϵ,X)+=([p,w],α)如果δ(q,b,X)包括(p,α)消耗buffer
Turing Machine
- 图灵机
- 有限个状态 (Q)
- 输入字母表 (Σ)
- 磁带字母表 (Γ)
- 转移函数 (δ)
- 开始状态 (q0)
- 空白符号 (B)
- 接受状态 (F)
- δ(q,Z)=(p,Y,D) D是方向direction
- 用αqβ表示一个状态,αβ代表从最左边非空到最右边非空的磁带,q指向刚刚被扫描的符号的左边,如果q在最右边,那么它在扫描B.
- L(M)={w∣q0w⊢∗I},I包含一个final state或者从I没有可选的ID
- 证明二者相等:
- final state->halting:
- 对于每个final state,移除所有移动
- 对于之前没有任何移动的非final state加上一个保护性的状态一直向后走
- halting->final states
- 添加一个新的final state
- 对于之前没有停止的,转移到final state
- 用图灵机定义的语言叫做Recursively Enumerable Languages
- 我们称一个按终止状态接受的,一定能停下来的图灵机叫做算法,算法能接受的语言是Recursive Language
- Multiple Tracks多个磁道,同一个磁头
- 半无限磁道,开始位置往右为合法位置
- 可以用两个栈模拟一个磁带,一个栈记录磁头左边的位置,一个栈记录磁头和磁头右边的位置
- 用2k个磁道可以模拟k个磁带,一个磁道用来记录位置
- 非确定性图灵机NTM
- Recursive & RE 语言的封闭性
- Union: 用两个磁带并行地模拟
- Intersection: 同样并行模拟
- Difference: Recursive可以并行模拟,但RE不行,因此不封闭
- 拼接:用一个两磁带的NTM,猜一个分割后并行模拟
- Star: 同样,猜许多的分割
- 反转:将输入反转再模拟
- 同态:将输入同态后再模拟
- 逆同态:构造一个NTM用于猜测x,使得h(x)=w
Decidability
- decidable⊂RE⊂all language
- 证明有些语言不是RE: 图灵机countable,但是所有语言uncountable
- 语言不可数:取出每一位都不相同的字符串
- 图灵机可数:任何由有限字符集组成的有限长度字符串的集合,都是可数的。
- 停机问题: HALT={<M,x>∣TM M halts on input x}
- 不可判定
- 假设TMH能够判定HALT
- 定义H′接受输入<M>
- 如果H接受<M,<M>>则循环
- 否则停机
- 考虑H′接受输入<H′>,
- 如果它停机,则证明H拒绝了<H′,<H′>>,不能停机
- 如果它不停机,则证明H接受<H′,<H′>>,代表其必须停机
- 冲突!!
- RE&Co-RE:
- Co−RE是一个RE语言的补集
- 如果一个语言既是RE又是Co-RE那么它是decidable
- decidable→RE and Co−RE : 如果L可判定,那么其补集可以通过反转接受和不接受来实现decidable
- decidable←RE and Co−RE: 并行模拟两个已有的图灵机即可
- Complexity
- TIme Complexity class: TIME(t(n))={L∣there exists a TM M that decides L in time O(t(n))}
- 对于多磁带的TM,每个t(n)有等价的O(t(n)2)的单磁带TM
- P,NP的定义:
- L={x∣∃y,|y|≤∣x∣k,<x,y>∈R} 则L∈NP
- CLIQUE问题
- 规约
- 给出一个新问题NEW,我们想判定它是否undecidable, 可以从一个已知的不可判定问题OLD转化到NEW,能够解决NEW的解法也可以用于解决OLD
- 如果我们想证明ATM={<M,w>:M accepts input w}不可判定:
- 那我们得假设A可判定,然后用A解决HALT问题
- <M,w>∈ATM 如果是的话那说明肯定HALT,如果不接受说明要么M拒绝w或者M在w上不停机
- 交换M中的接受和拒绝状态,再次判定,如果是的话说明肯定是拒绝,HALT;否则不是HALT
- Rice′s Theorem一切不平凡的TM性质都是undecidable的!
- NP问题的规约,SAT,3SAT问题
迁移系统
- 迁移系统A=<S,S0,T,α,β>
- S是状态集合
- S0⊂S是初始状态集
- T是一个转移集合
- α,β是两个从T到S的映射,α(t)代表迁移的源,β(t)代表迁移的目标
- 路径是t1,t2...,tn使得∀i,1≤i≤n,β(ti)=α(ti+1)∧α(t1)∈S0
- 如果存在t∈T,α(t)=s∧β(t)=s′则称s→s′; s↠s′ 代表经过一个路径
- 可达状态&终结状态 α,β 拓展到路径上,路径的偏积(路径拼接起来),定义ϵs长度为0,起终点都是s
- 带标签的迁移系统A=<S,S0,T,α,β,λ>其中λ是把T中的每一个迁移映射成A的标签λ(t) (标签可能代表触发这个迁移的行为或者事件); trace(c)=λ(t1)λ(t2)...代表路径的踪迹
- 迁移系统的同态:
- A=<S,S0,T,α,β>,A′=<S′,S0′,T′,α′,β′>
- 同态是一个映射的二元组(hσ,hτ) 其中: hσ:S→S′,hτ:T→T′ 满足对于T中的每一个转移t: α′(hτ(t))=hσ(α(t)),β′(hτ(t))=hσ(β(t))
- 如果hσhτ都满射那么同态h满射; 如果h是从A到A′的满射同态,那么A′是A在h下的商
- 迁移系统的同构:
- hσ和hτ都双射,则称强同构
- 如果对于每个可达的状态得到的可达子迁移系统强同构,那么称原本的两个迁移系统是弱同构的
- 双模拟等价: A=<S,S0,T,α,β>,A′=<S′,S0′,T′,α′,β′>
- 存在一个二元关系B⊂S×S′ 使得B(S0,S0′)并且如果B(s1,s1′)且s1→s2则存在一个s2′∈S′使得s1′→s2′且 B(s2,s2′)
- 不一定双射,可能多对一
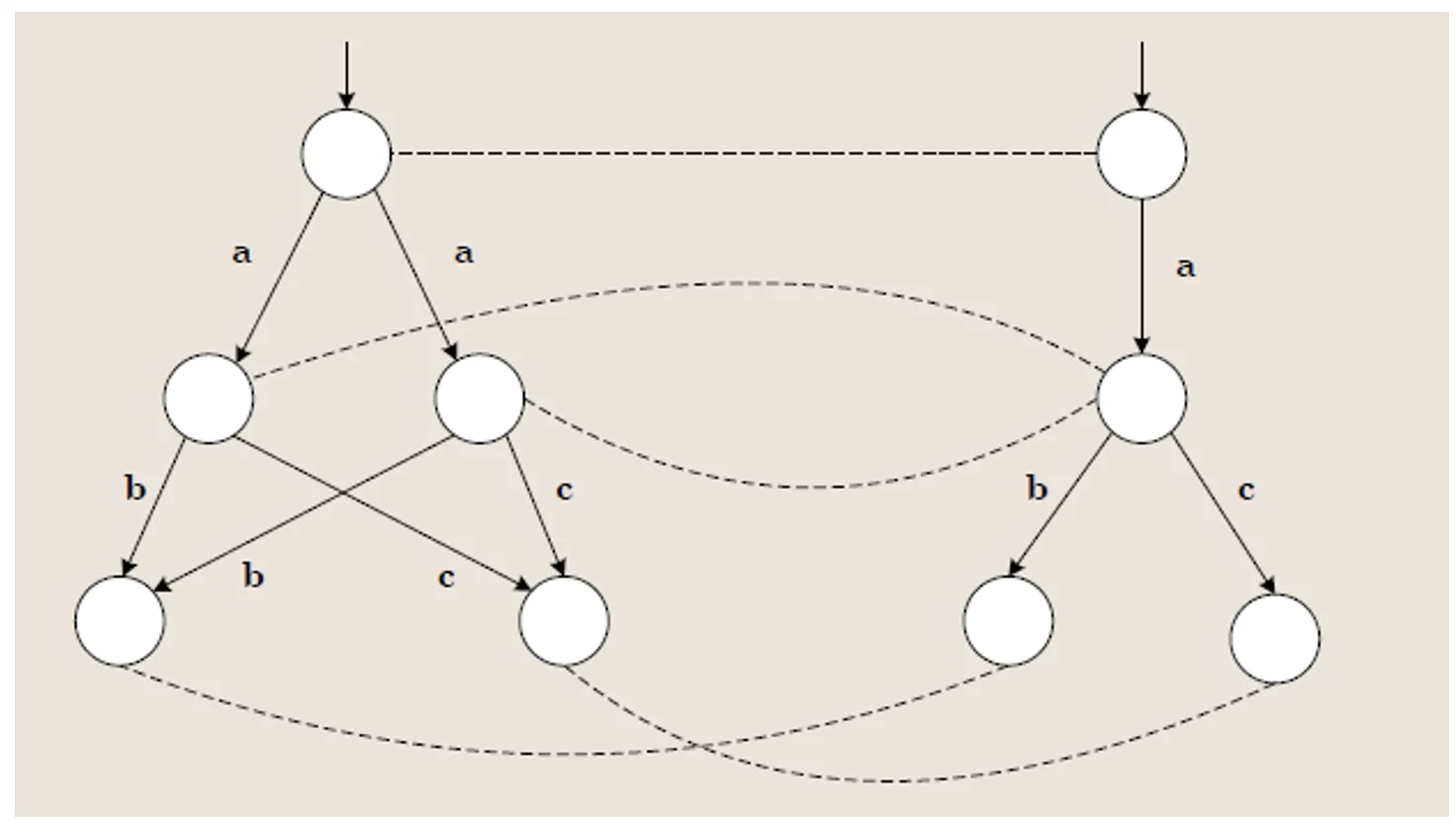 满足双模拟
满足双模拟
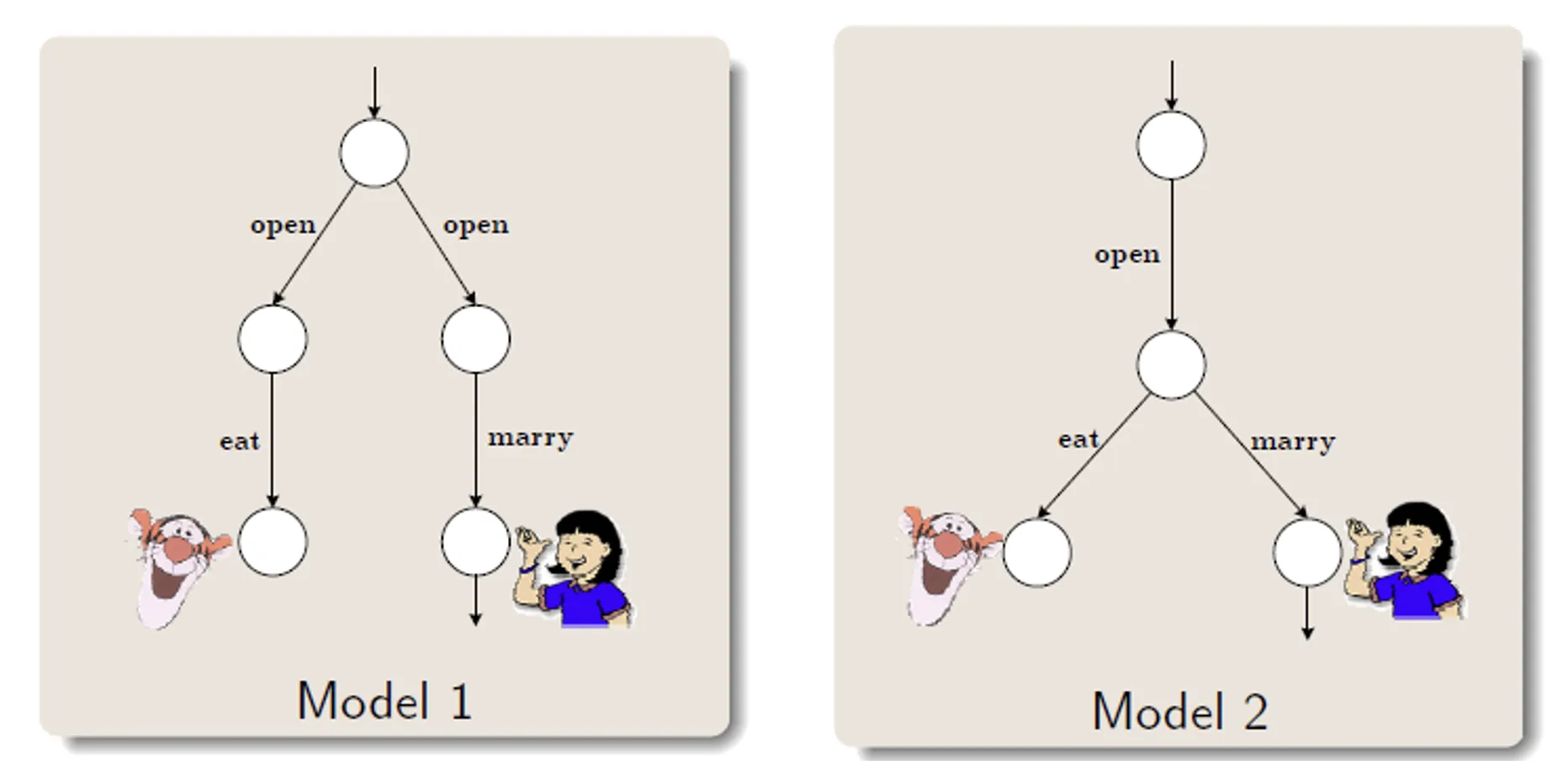 不满足双模拟(仔细看右边的节点并不能对应左边的任一节点,因为左边只有一个转移)
不满足双模拟(仔细看右边的节点并不能对应左边的任一节点,因为左边只有一个转移)
- 迁移系统的运算
- 自由积(每个系统在每个时刻都执行一步迁移)
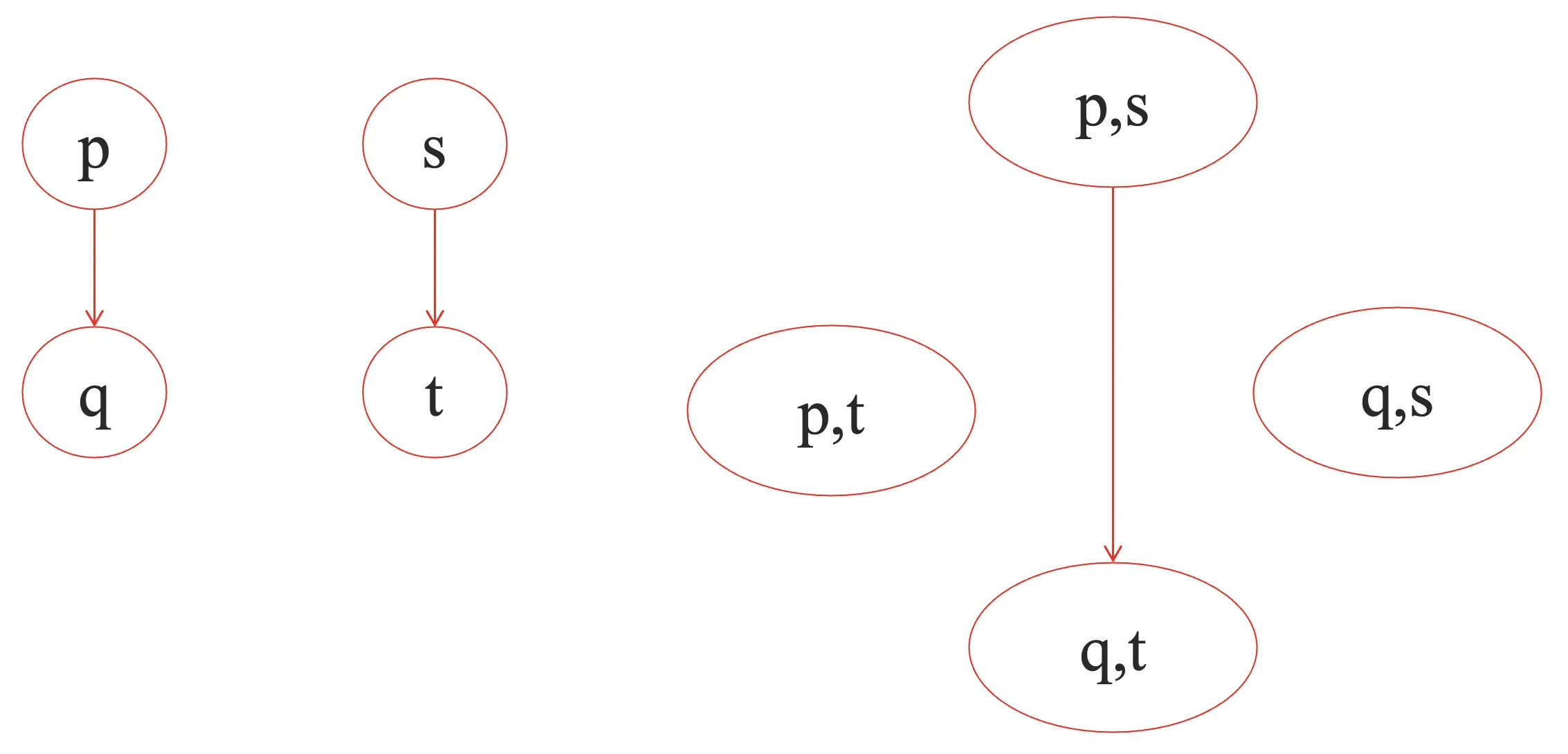
- 同步积(限制可以同时发生的迁移)同步限制<a,b>
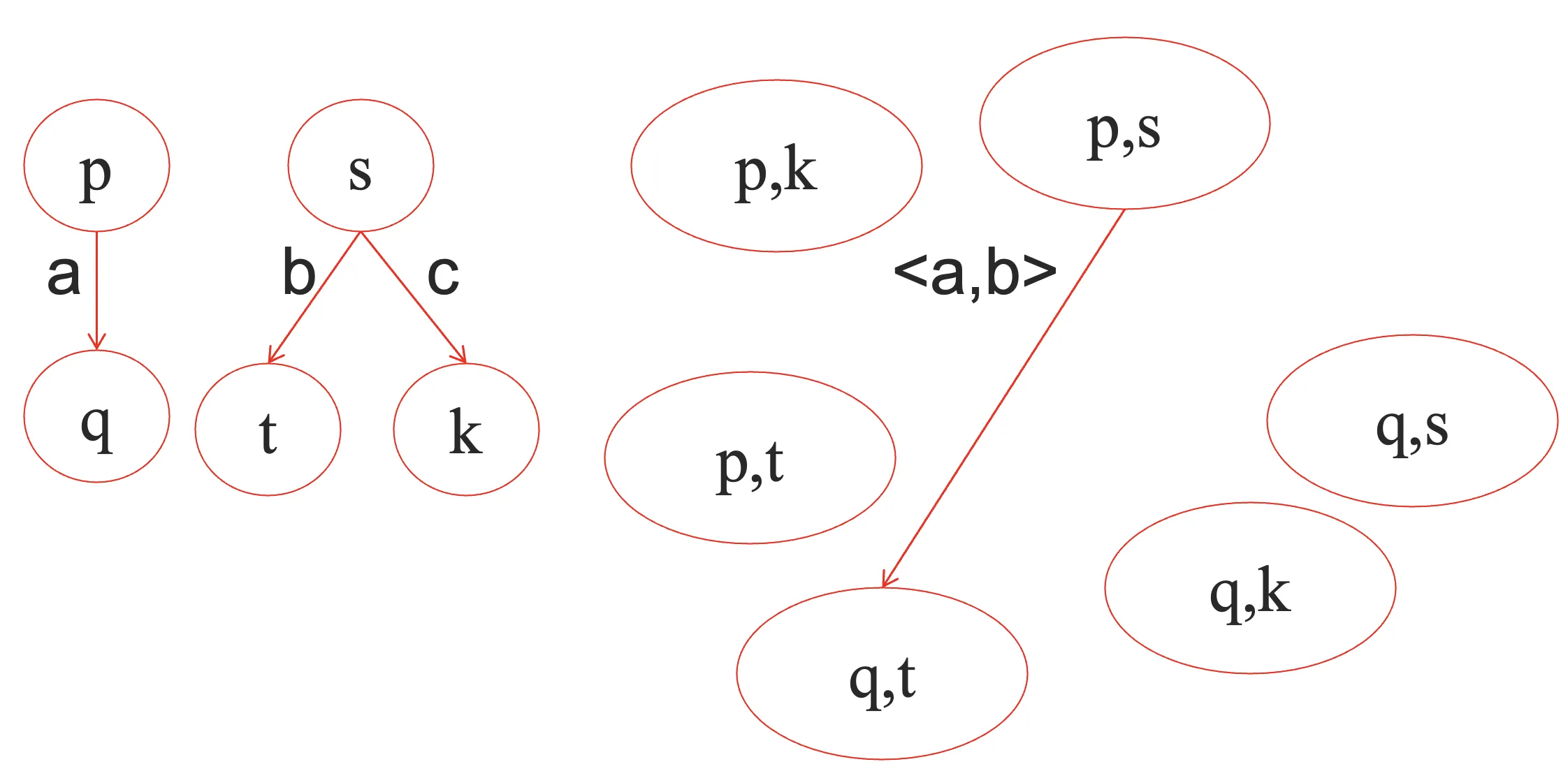
- 可以引入τ迁移,每个状态都有一个自环转移,这样同步积就不一定要进行实质上的转移了
- 也可以对于同步积,对于每个限制,用同样的标签来表达这两个转移必须同时发生
- 建模
- 一个程序的建模可以通过变量的值和pc寄存器来捕捉。
- 转移是x的值,{}代表为真的命题
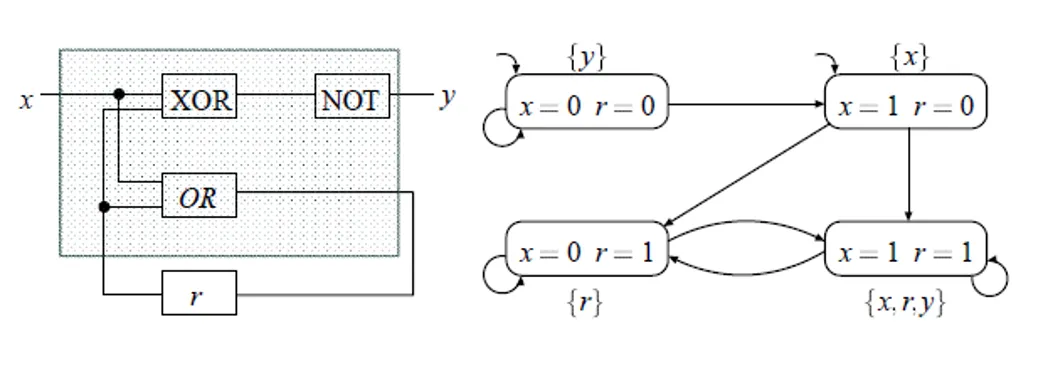
- 计算树逻辑
- 计算树展现了从初始状态开始所有可能的执行路径,CTL∗(Computation Tree Logic)公式描述了计算树的性质,由路径量词和时序操作符组成
- 路径量词有两个:
- A 表示被修饰的逻辑公式对于所有路径成立
- E ..某些路径成立
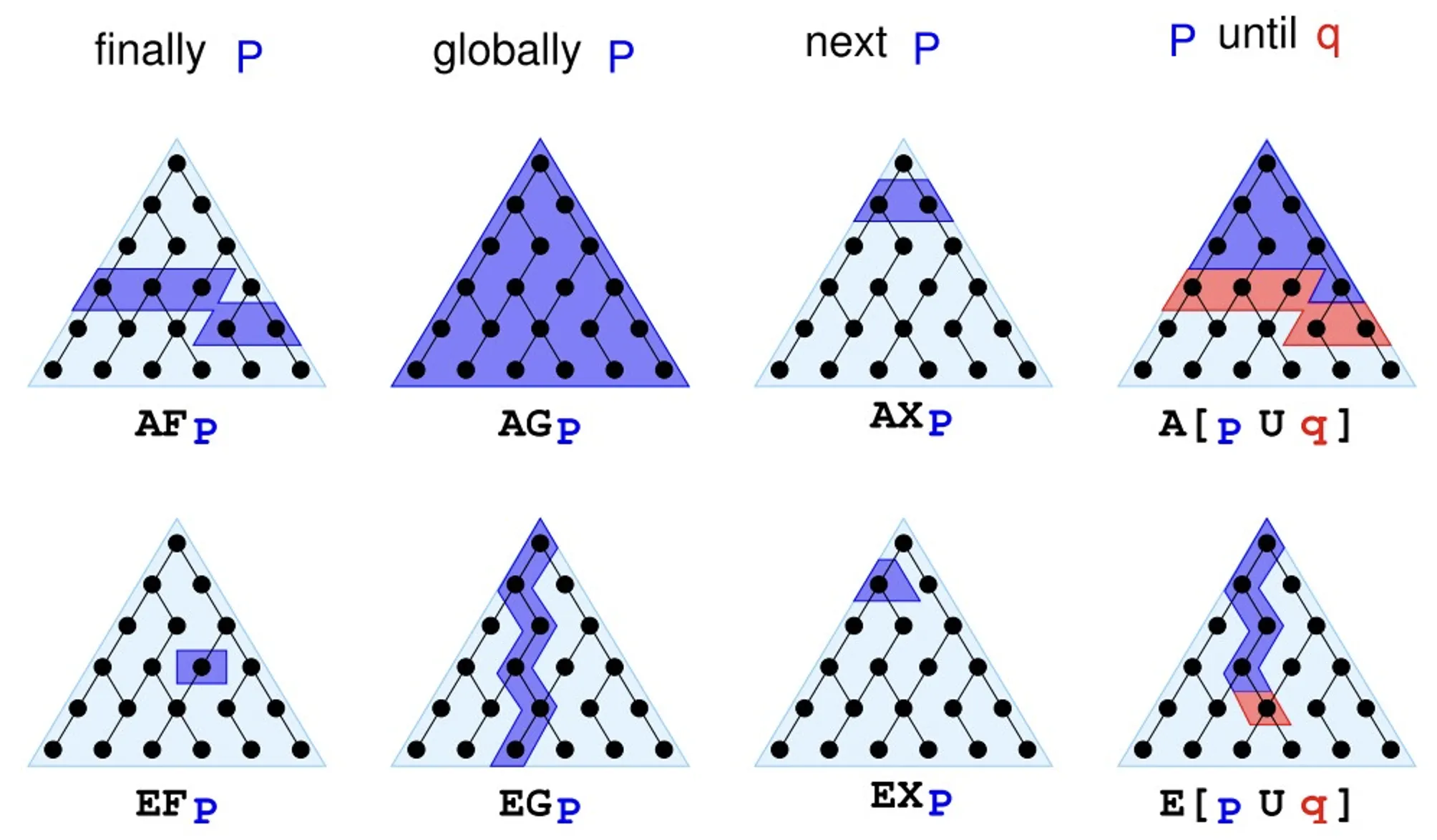
- 时序操作符有五个:
- X: Xp 表示p在路径的下一个状态成立
- F: Fp 表示p在路径的将来的某个状态成立
- G: Gp表示p在路径的全部状态下都成立
- U: pUq表示p成立直到q成立为止 U代表q一定会成立
- R: pRq表示p成立直到q成立为止(包括q成立这个状态)
- 状态公式(在某个特定状态下成立)
- 如果p∈AP那么p是一个状态公式,其中AP表示愿自命题
- 如果f和g是状态公式,那么¬f,f∧g,f∨g也是
- 如果f是一个路径公式,那么Ef和Af是状态公式
- 路径公式的语法:
- 如果f是一个状态公式,那么f也是一个路径公式
- 如果f和g是路径公式,那么¬f,f∧g,f∨g,Xf,Ff,Gf,fUg,fRg 也是
- 如果f状态,s→f意味f在状态s下保持
- 如果g路径,π→g意味g沿着路径π下保持
- CTL是CTL*的一个严格子集,只允许分时逻辑,每个限行时间的操作符G,F,X,U,R 都必须立即被一个路径量词修饰。(A,E)
- LTL是线性时序逻辑,组成LTL的逻辑公式都形如Af其中f路径
Petri网
- Petri网是一个四元组C=(P,T,I,O)
- P是地址的集合,P={p1,p2,...,pn}
- T是转移的集合,T={t1,t2,...tm}
- I:T→2P是从迁移到输入地点的映射,一个迁移可以有不止一个输入地点
- O:T→2P是从迁移到输出地点的映射,一个迁移可以有不止一个输出地点
- 每个地点都有token
- 当一个转移的所有输入地点有一个token时,称这个转移被赋能了。一次点火使得输入的token数量都-1,所有输出地点的token数量+1
- 一次运行指点火的序列
- 基本性质
- 顺序执行,同步,汇合,分叉,并发,非确定性,冲突
- 带权边:必须拥有w(fi)个令牌才允许执行
- 有限容量:每个地点pi最多容纳K(pi) ,但可以通过再建模一个地点用于表示地点p的空位数来利用无限容量Petri网模拟有限容量Petri网
- 建模
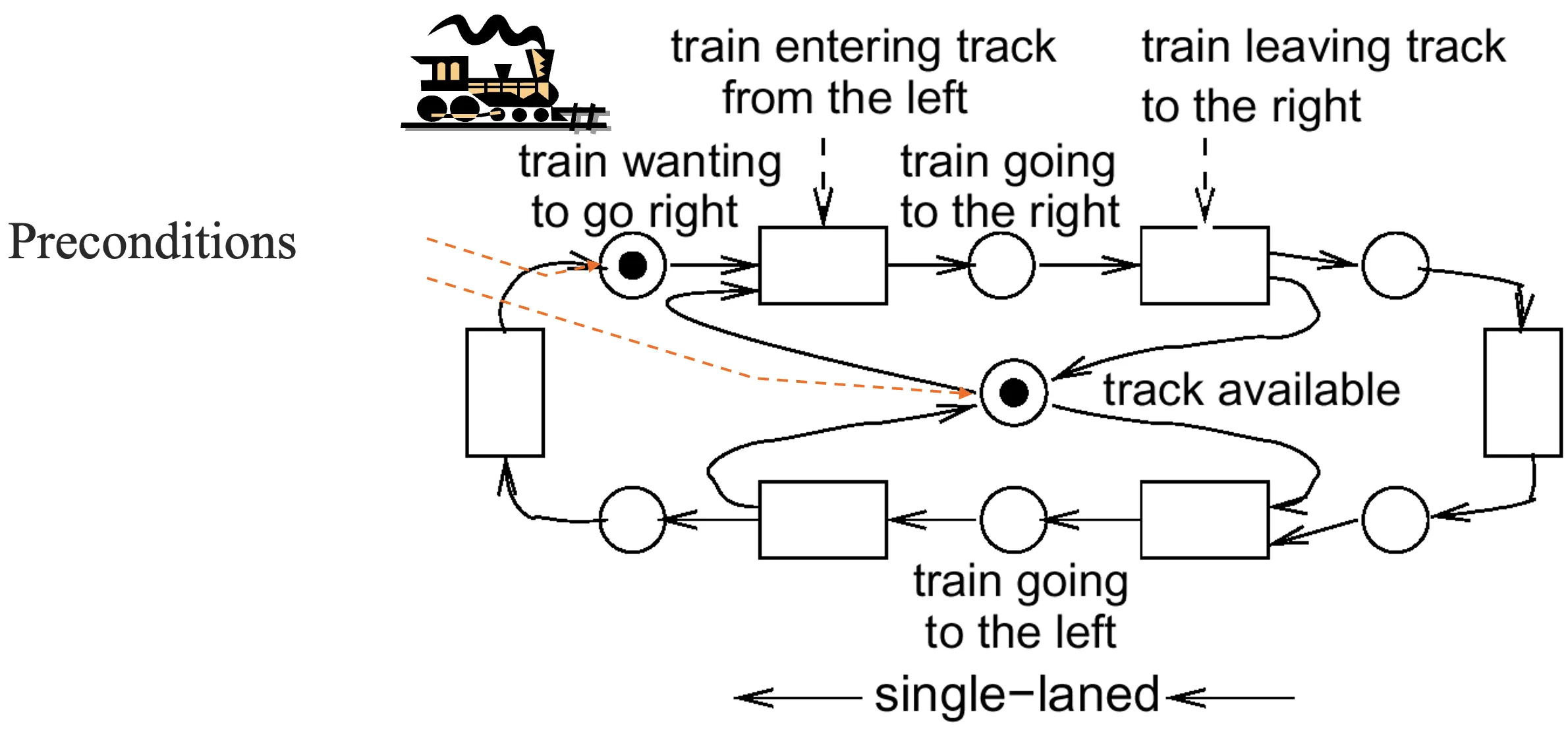
- 单个轨道铁路段同步
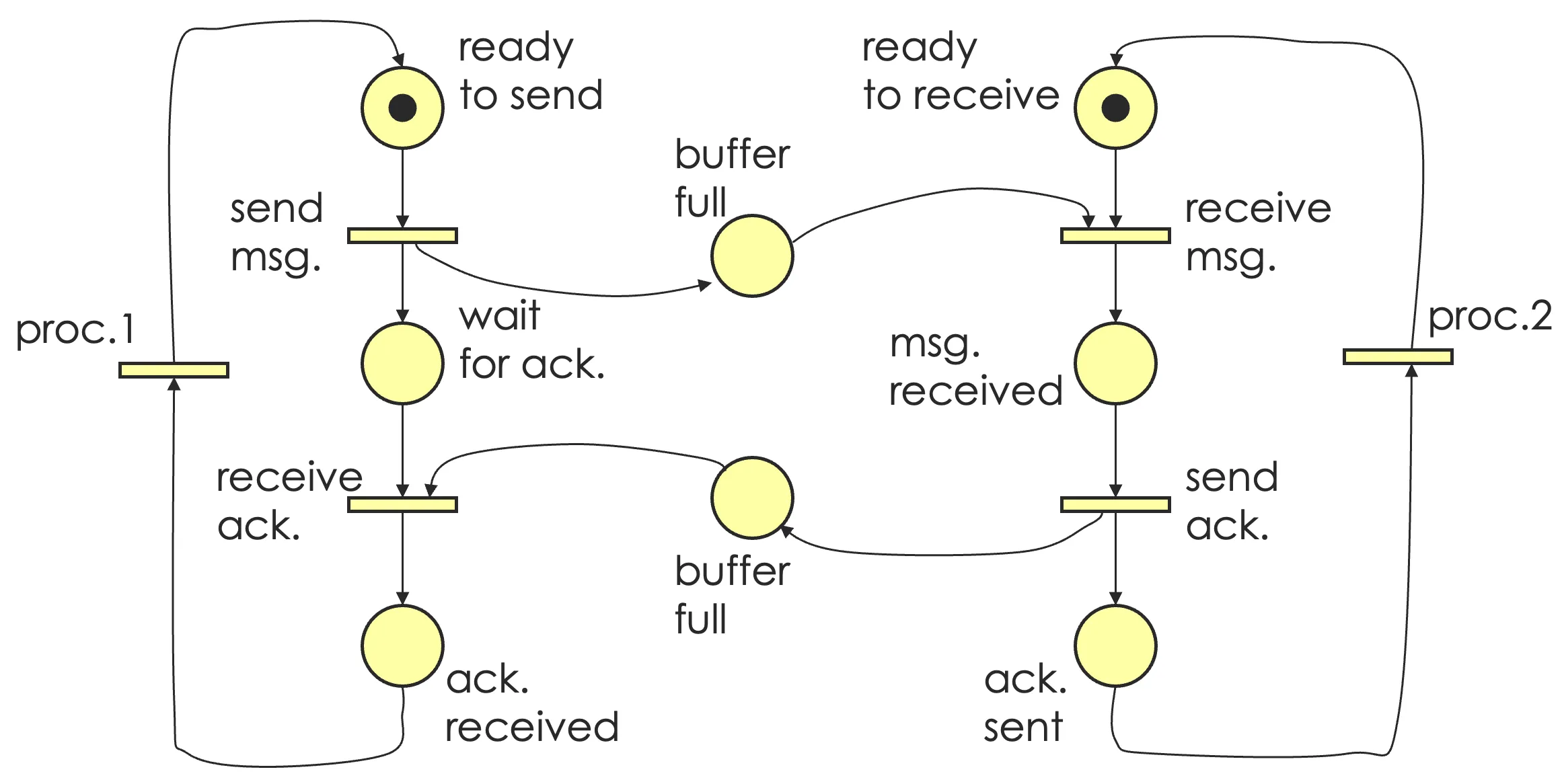
- 建模通信协议
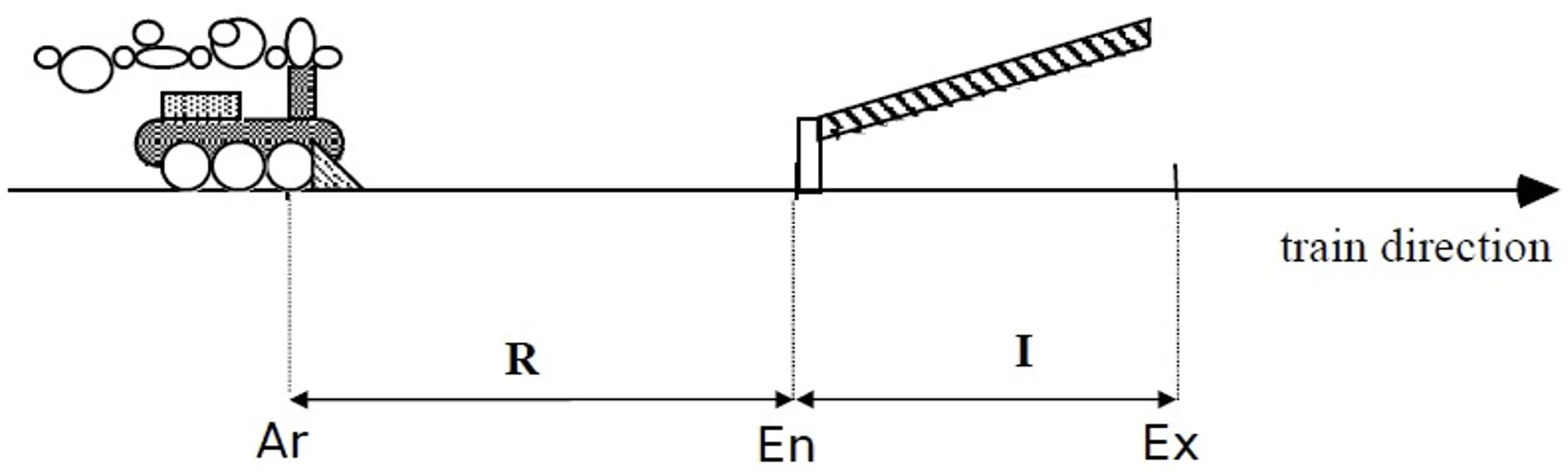
- 时间Petri网在每一个转移中关联了一个时间区间[a,b],相对于转移最后一次被赋能来说的,假设t在时间c被赋能,那么t只能在[c+a,c+b]点火,点火不消耗时间,并且最迟必须在时间c+b点火,除非被其他转移失能了
- 建模
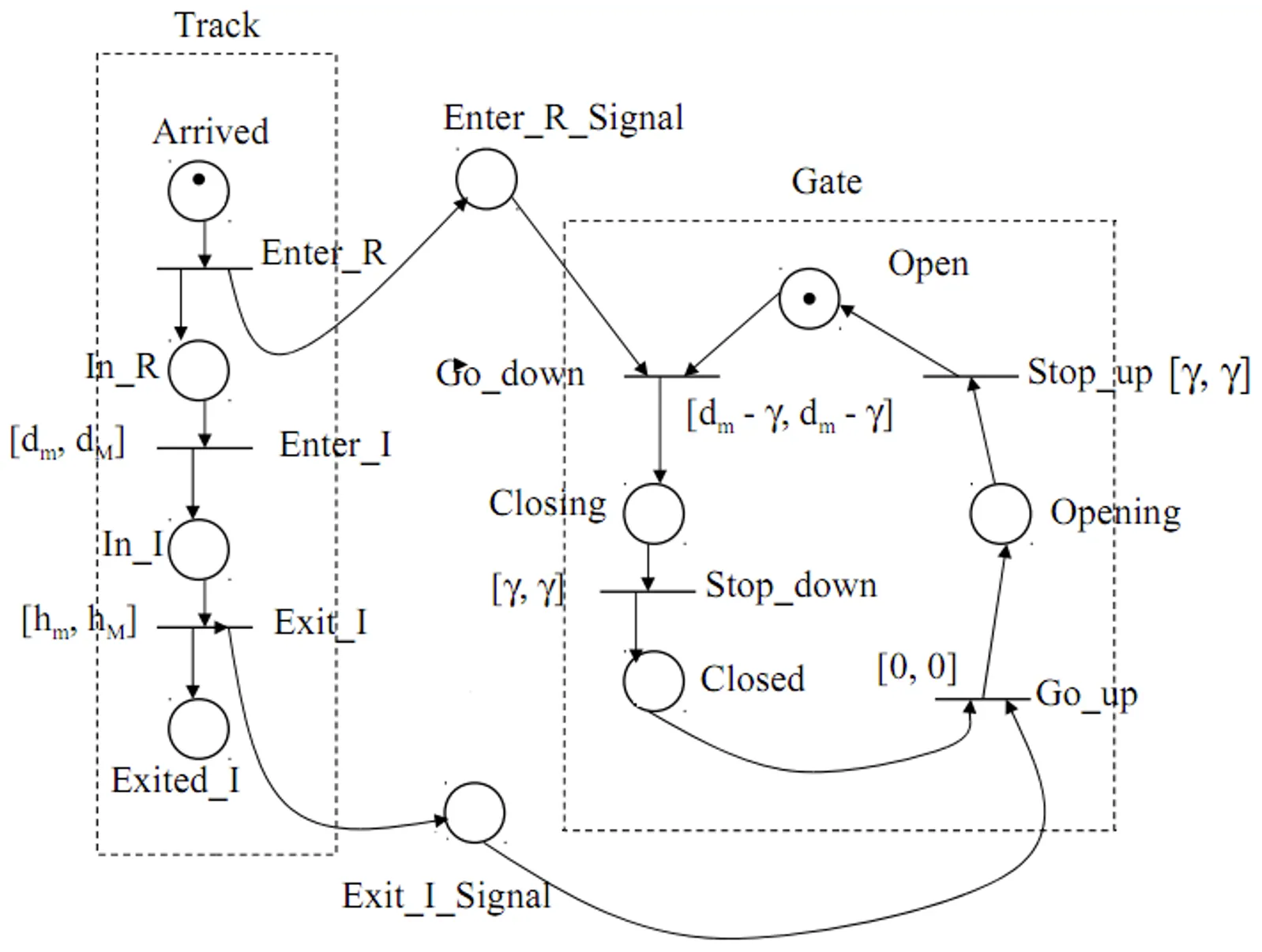
时间自动机
- 时间流逝只发生在节点处,每个节点有不变式,转移有满足的条件和执行的操作
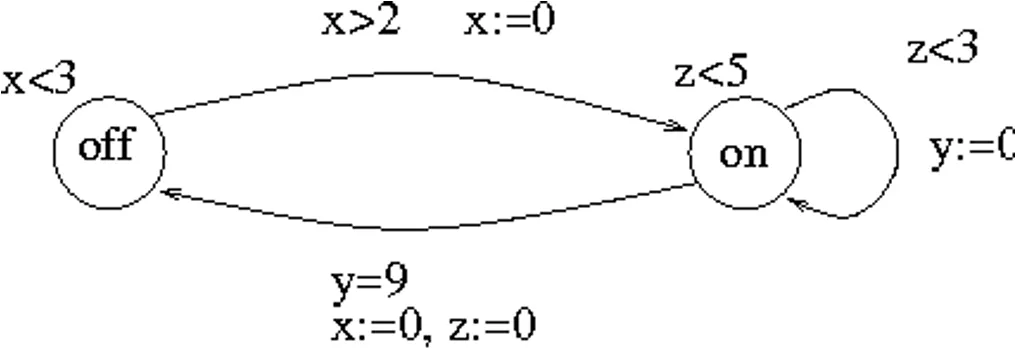

 满足双模拟
满足双模拟
 不满足双模拟(仔细看右边的节点并不能对应左边的任一节点,因为左边只有一个转移)
不满足双模拟(仔细看右边的节点并不能对应左边的任一节点,因为左边只有一个转移)