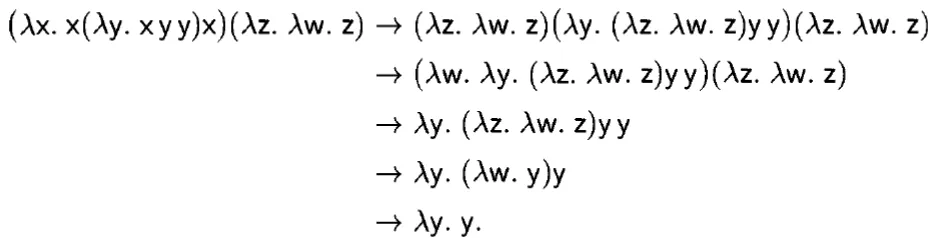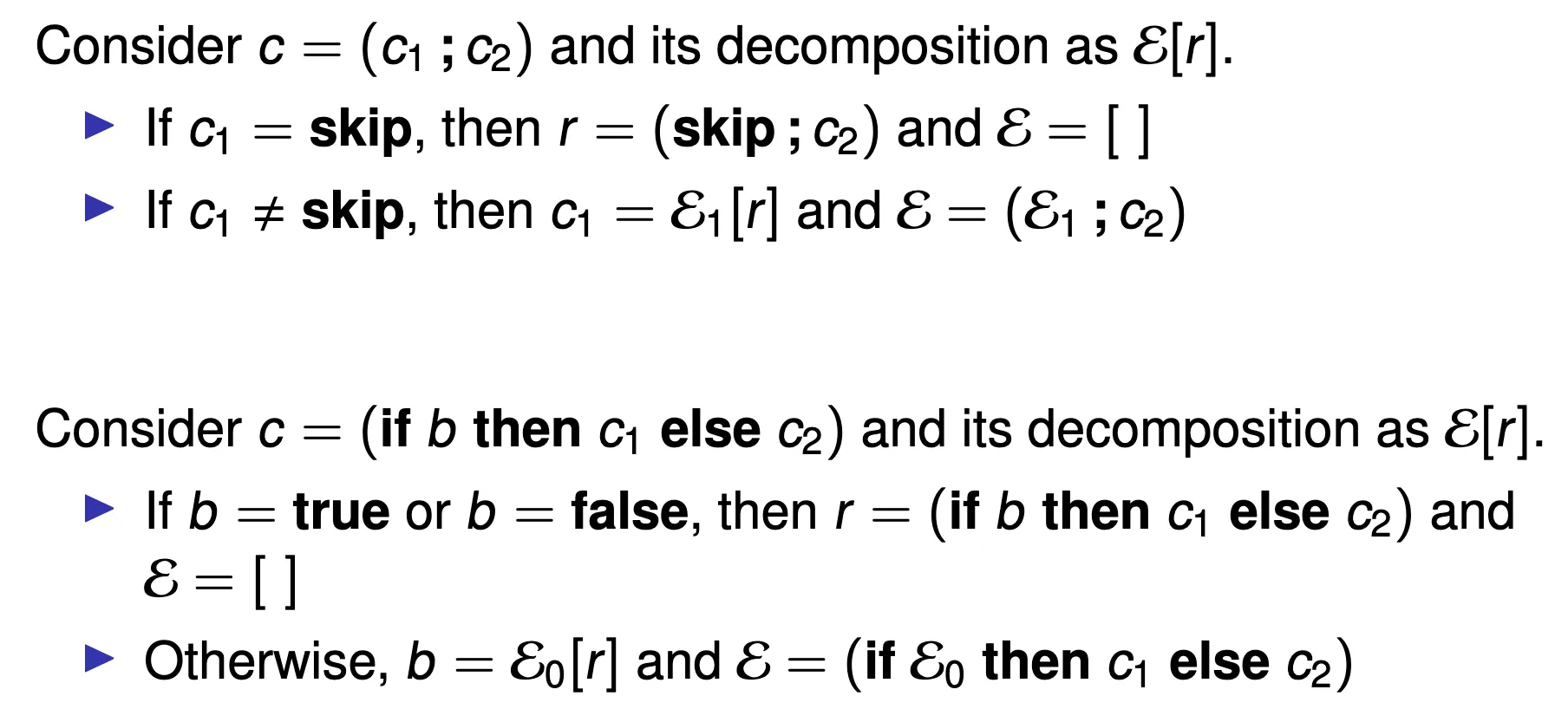Credit

• 授课教师： 梁红瑾
• 上课时间：2025秋
• 主要是分成lambda calculus和semantics两部分

Lambda Calculus

之前就听说过不少，SICP课上还被Church Numeral折磨过

定义

$(Terms) M,N\ ::=\ x\ | \lambda x.M\ |\ M\ N$

规则

• $\lambda$延伸到括号的最右方 $\lambda x.\ M\ N$意思是$\lambda x.\ (M\ N)$
• 函数应用是左结合 $M\ N\ P$意思是$(M\ N)\ P$

自由和约束变量

• $\lambda x.(x+y)$相等于$\lambda z.(z+y)$, $x$是绑定变量(bound variables)
• 但自由变量的名字很重要
• fv(M)是M中自由变量的集合
  • $fv(x) \overset{\mathrm{def}}{=} {x}$
  • $fv(\lambda x.M) \overset{\mathrm{def}}{=} fv(M)-{x}$
  • $fv(M\ N) \overset{\mathrm{def}}{=} fv(M) \cup fv(N)$
• $\alpha$等价: $\lambda x.M=\lambda y.M[y/x]$ y是新变量

化简规则

• $\beta$化简： $(\lambda x.M)N \rightarrow M[N/x]$
• 替换规则
  • $x[N/x] \overset{\mathrm{def}}{=} N$
  • $y[N/x] \overset{\mathrm{def}}{=} y$
  • $(M P)[N/x] \overset{\mathrm{def}}{=} (M[N/x]) (P[N/x])$
  • $(λx.M)[N/x] \overset{\mathrm{def}}{=} λx.M$
  • $(λy.M)[N/x] \overset{\mathrm{def}}{=} λy.(M[N/x]), if\ y ∉ fv(N)$
  • $(λy.M)[N/x] \overset{\mathrm{def}}{=} λz.(M[z/y][N/x]), if\ y ∈ fv(N)\ and\ z\ fresh$

合流性

Terms可以以任何顺序化简，如果有最终结果的话，其唯一确定。

• $\beta-redex$ 类似$(\lambda x.M)N$形式的term
• $\beta-normal\ form$ 不含$\beta-redex$的term
• 合流性理论:
  • 对于所有的$M,M_1,M_2$,如果$M\rightarrow^*M_1$且$M\rightarrow^*M_2$,那么存在$M'$使得$M_1\rightarrow^*M'$且$M_2\rightarrow^*M'$
• $Normal-order\ reduction:$最外层的最左边的redex(有点像lazy evaluation)
  • $(\lambda u.\lambda v.v)((\lambda x.x\ x)(\lambda x.x\ x))\rightarrow \lambda v.v$
• $Applicative-order\ reduction:$最内层的最左边的redex(有点像eager evaluation)
  • $(\lambda u.\lambda v.v)((\lambda x.x\ x)(\lambda x.x\ x))\rightarrow (\lambda u.\lambda v.v)((\lambda x.x\ x)(\lambda x.x\ x)) ...$

求值和化简

• 化简可以在lambda函数体内化简，但是求值不在lambda函数体内化简
• 下图中evaluation会停在第三个后
• 
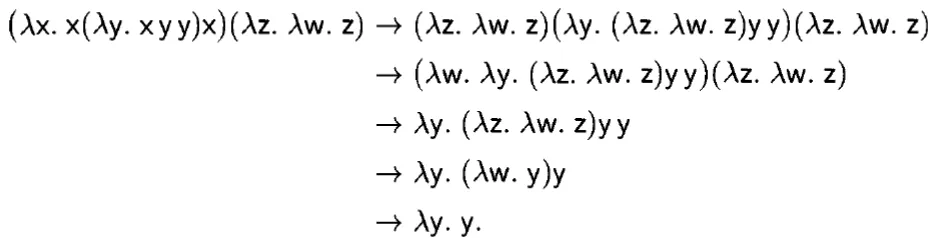
• 范式(canonical form)意思是不能再求值的form, 但可能范式内部（lambda内部）可以继续化简

对于常用值的编码

• $True \overset{\mathrm{def}}{=} \lambda x.\lambda y.x$
• $False \overset{\mathrm{def}}{=} \lambda x.\lambda y.y$
• True是取第一个, False是取第二个，因此在此上面进行的运算也是根据这个性质进行的
• $0 \overset{\mathrm{def}}{=} \lambda f.\lambda x.x$
• $n \overset{\mathrm{def}}{=} \lambda f.\lambda x.f^n\ x$
• n是运算n次

不动子

• $F = \lambda f.\,\lambda n.\,\text{if }(n=0)\text{ then }1\text{ else } n \cdot f(n-1).$ 则$fact = F\ fact$
• 图灵不动子
  • $A\ =\ \lambda x.\lambda y.y(x\ x\ y)$, $\Theta=A A$
• Curry不动子
  • $Y=\lambda f.(\lambda x.f (x\ x)) (\lambda x.f (x\ x))$

Simply-Typed Lambda Calculus

定义

• $(\text{Types})\quad \tau, \sigma ::= T \mid \sigma \to \tau$
• $\Gamma \vdash M : \tau$. $\Gamma$中有所有的自由变量定义

Soundness

• 对于任何$M,M',\tau$如果$· \vdash M:\tau$且$M\to^*M'$那么$· \vdash M':\tau$并且要么$M'\in Values$或者$\exist M''.M'\to M''$
• Preservation: M,M' and $\tau$, 如果$·\vdash M:\tau$且$M\to M'$那么$·\vdash M':\tau$
• Progress:如果$· \vdash M:\tau$那么要么$M\in Values$或者$\exist M'.M\to M'$

Not Complete

• 这个类型系统可能会拒绝不会出错的程序
• 有完善类型的term永远会终止

Curry-Howard同构

• 如果把基础类型看成命题，函数类型看成蕴含，乘积类型看成and，那么构造性命题逻辑和类型系统同构！
• 测试类型是否非空:(对应的term是否closed)
  • 看这个对应的命题是否能被证明
• 排中律：在命题逻辑中，一个命题要么真要么假，因此命题$p\lor(p\to q)$永远为真。
  • 但是STLC不支持这一点，它要求必须确定或两边到底哪个为真。因此如果需要用到它，则必须把它作为一个明显的假设

操作语义

我们希望探寻语句究竟怎么算

定义

• $(States)\quad \sigma \in Var \to Values$
• $(IntExp)\quad e::=\textbf{n}|x|e+e|e-e|...$
• $(Comm) c::=\textbf{skip}|x:=e|c;c|\textbf{if}\ b\ \textbf{then}\ c\ \textbf{else}\ c|\textbf{while}\ b\ \textbf{do}\ c$
• 注意while的小步语义不要丢失b

小步语义的性质

• 对于所有$c,\sigma,c',\sigma ',c'',\sigma ''$, 如果$(c,\sigma)\to(c',\sigma ')$并且$(c,\sigma)\to (c'',\sigma '')$, 那么$(c',\sigma ')=(c'',\sigma '')$ 确定性
• 对于所有$c,\sigma,c',\sigma ',c'',\sigma ''$, 如果$(c,\sigma)\to^*(c',\sigma ')$并且$(c,\sigma)\to^* (c'',\sigma '')$, 那么存在$c''',\sigma'''$使得$(c',\sigma ')\to^*(c''',\sigma ''') and (c'',\sigma '')\to^*(c''',\sigma ''')$ 合流性
• $(e,\sigma)$和$(b,\sigma)$是normalizing的（最终会到达一个normal form），但$(c,\sigma)$不一定

拓展

• 直接对表达式求值
• 
• 我们不希望把局部变量暴露给$\sigma$因此对于局部变量定义
  • 
  • 仍然包裹局部变量定义，但执行一步
• 添加堆
• Contextual Semantics
  • 我们考虑用[]指代下一步要算的redex即原子操作，
  • $\mathcal{E} ::= [\,]\mid \mathcal{E} + e\mid \mathcal{E} - e\mid n+\mathcal{E}\mid n - \mathcal{E}$
  • $x:=1+[\ ]\ NOT\ while\ false\ do\ x:=1+[\ ]$ (不该出现)
  • 

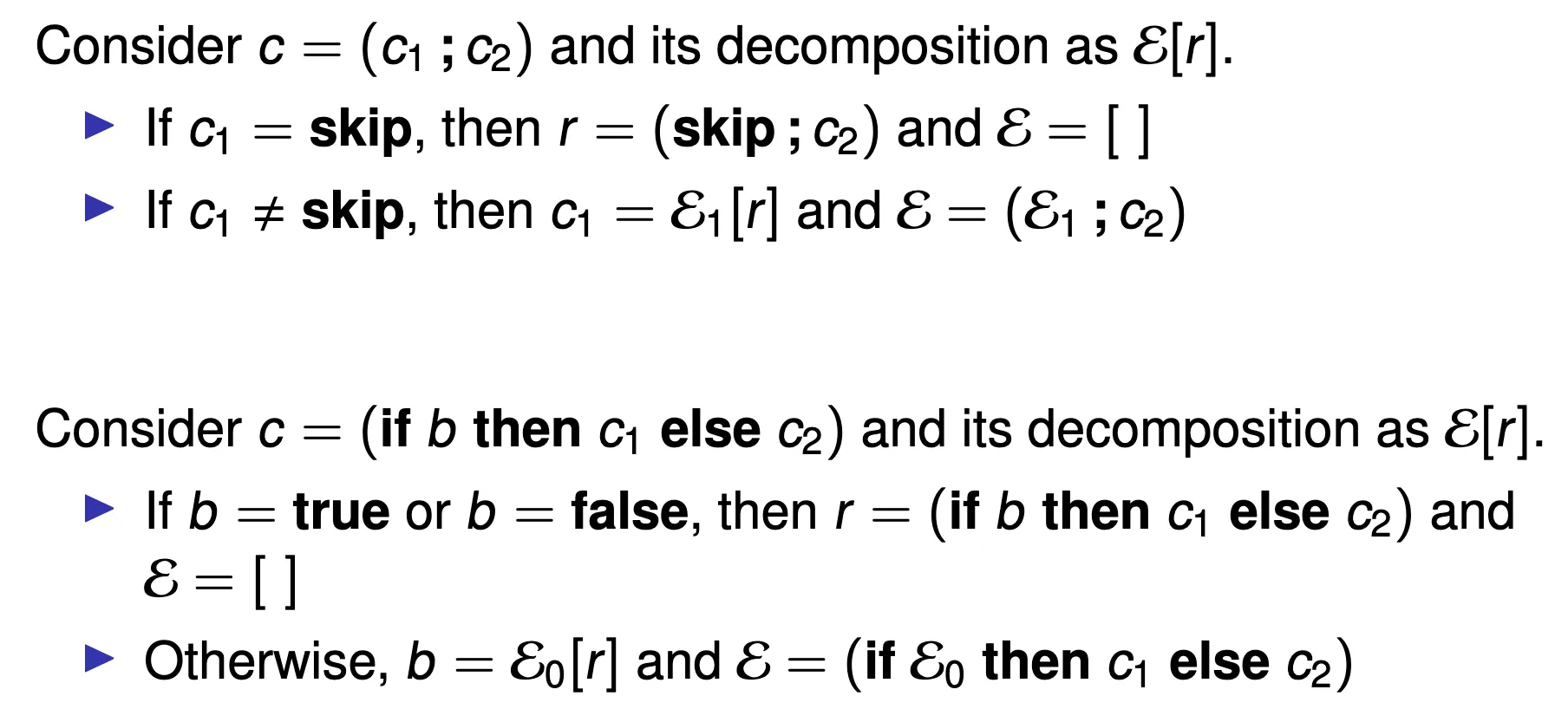
大步语义

• 直接得知最后的结果
• $(c,\sigma)\Downarrow \sigma';(e,\sigma)\Downarrow n$
• For all $e,\sigma,n,n',$ 如果$(e,\sigma)\Downarrow n$且$(e,\sigma)\Downarrow n'$那么$n=n'$ 确定性
• 对于所有$e,\sigma$存在$n$使得$(e,\sigma)\Downarrow n$ 整体性Totality
• $(e,\sigma)\lfloor \textbf{n}\rfloor\ iff.\ (e,\sigma)\to^*(\textbf{n},\sigma)$和小步语义等价

霍尔逻辑

定义

• 偏正确性定义: $\{p\}c\{q\}$
• 全正确性定义: $[p]c[q]$ (偏正确性+一定终止)

核心规则

• AS: $\{p[e/x]\}x:=e\{p\}$
• 增强前条件、减弱后条件
• 循环不变式:
  • $\{i\land b\}c\{i\}$
  • 有时候需要增强loop invarient来证明循环后的内容
• 循环变量:
  • $[i\land b\land (e=x_0)]c[i\land(e<x_0)]$ $i\land b \Rightarrow e\ge0$
  • 递减且有界
• 在应用顺序规则的时候，需要先标注出二者之间的条件(assertation)

Soundness and completeness

• 注意$|-$和$|=$的区别，$|-$是在某个公理系统中可以推导出来的,$|=$代表在某个配置下是真的
• Soundness: 如果$|-p$那么$|=p$
• Completeness: 如果$|=p$那么$|-p$
• 我们可以证明Soundness: 如果$|-\{p\}c\{q\}$那么$|=\{p\}c\{q\}$
  • 先对于公理证明
  • 然后利用小步语义进行归纳法
• 但是霍尔逻辑并不complete:
  • 
  • 如果complete的话，那么任意语义为真的命题都能被证明(与哥德尔不完备定理冲突)
  • $|=\{\textbf{true}\}c\{\textbf{false}\}$ 当且仅当c不停止才成立，然而c是否停止是不可判定的
• 因此提出Relative Completeness相对完备，如果我们把所有语义为真的命题作为已知条件，那么completeness成立