强化学习基本组件

Policy Gradient 学习Actor

策略Policy一般用 $\pi$ 表示, 用 $\pi_\theta$ 来表示参数为 $\theta$ 的策略
策略的输入通常是对环境的一个观察，输出是动作的概率分布
我们可以这样建模一次完整的轨迹Trajectory(也许是你玩游戏的一次通关过程)
- $s_i$ 第i次的环境状态
- $a_i$ 第i次针对 $s_i$ 采取的动作
- $\tau=$ { $s_1$ , $a_1$ , $s_2$ , $a_2$ ,...}就建模出了一个轨迹
- $p_\theta(\tau) = p(s_1) p_\theta(a_1|s_1) p(s_2|s_1, a_1) p_\theta(a_2|s_2) p(s_3|s_2, a_2) \cdots = p(s_1) \prod_{t=1}^{T} p_\theta(a_t|s_t) p(s_{t+1}|s_t, a_t)$
在轨迹的中间可能会有Reward, 我们将这条轨迹上的所有Reward相加就是这条轨迹的总Reward, 称为 $R(\tau)$
很显然，我们想优化参数 $\theta$ 下的所有轨迹的期望Reward, $\overline{R}_\theta = \sum_{\tau} R(\tau) p_\theta(\tau) = \mathbb{E}_{\tau \sim p_\theta(\tau)} \left[ R(\tau) \right]$
如果我们对 $R_{\theta}$ 求梯度

\nabla \overline{R}_\theta = \sum_{\tau} R(\tau) \nabla p_\theta(\tau) = \sum_{\tau} R(\tau) p_\theta(\tau) \frac{\nabla p_\theta(\tau)}{p_\theta(\tau)}

= \sum_{\tau} R(\tau) p_\theta(\tau) \nabla \log p_\theta(\tau)

= \mathbb{E}_{\tau \sim p_\theta(\tau)} [R(\tau) \nabla \log p_\theta(\tau)] \approx \frac{1}{N} \sum_{n=1}^N R(\tau^n) \nabla \log p_\theta(\tau^n)

= \frac{1}{N} \sum_{n=1}^N \sum_{t=1}^{T_n} R(\tau^n) \nabla \log p_\theta(a_t^n | s_t^n)

假如所有的Reward都是正的, 那根据上述式子，我们会根据梯度增大所有采样到的 $p_\theta$ 的值。但是，没有采样到的动作的概率就会下降，但也许没有采样到的动作更好.
所以我们可以对于Reward设立一个Baseline，采样到的Reward减去baseline再代入到式子中：

\nabla \overline{R}_\theta \approx \frac{1}{N} \sum_{n=1}^{N} \sum_{t=1}^{T_n} \left( R(\tau^n) - b \right) \nabla \log p_\theta(a_t^n | s_t^n) \qquad b \approx \mathbb{E}[R(\tau)]

这里的 $R(\tau^n) - b$ 被称为优势,Advantage,用A表示

如果以轨迹为单位来分配Reward，一条轨迹上的所有动作的Reward都相同, 不利于细粒度的优化. 实际上，通常一条轨迹上的不同动作的贡献都是不同的. 我们可以采用每个动作的奖励是这个动作的所有Reward之和.
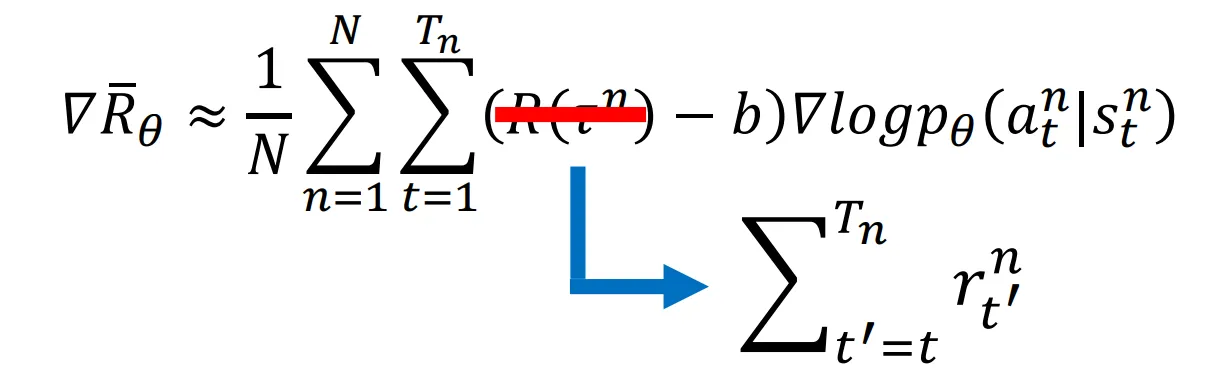
当然, 第一个动作可能不会对最后一个奖励产生特别大的影响, 所以也可以在求和项之前加上指数衰减的权重，但这个权重还是得看实际情况.

\mathbb{E}_{x \sim p}[f(x)] = \int f(x) p(x) dx = \int f(x) \frac{p(x)}{q(x)} q(x) dx = \mathbb{E}_{x \sim q} \left[ f(x) \frac{p(x)}{q(x)} \right]

这样就把服从q分布的数据迁移到p分布上了

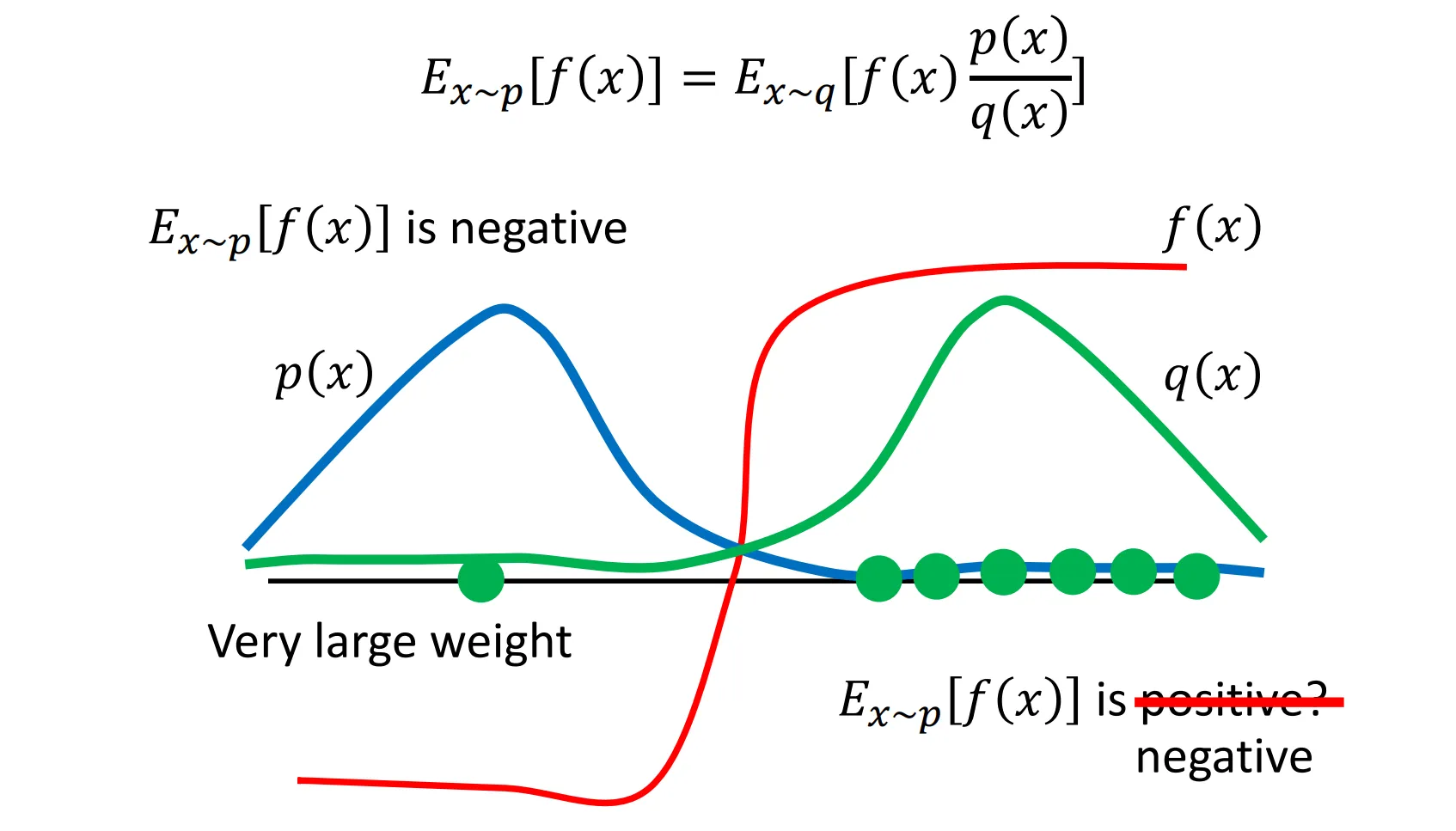如图，本来是负的期望因为采样原因，如果根据q分布全部采样到了右边的点，可能误把期望变成正值

衡量的是“用分布Q去近似分布P时，所造成的信息损失。

D_{KL}(P \| Q) = \sum_{x} P(x) \log \frac{P(x)}{Q(x)}

J^{\theta'}_{PPO}(\theta) = J^{\theta'}(\theta) - \beta KL(\theta, \theta')

PPO2: 裁剪了比例，防止更新过大

L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min(r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1-\epsilon, 1+\epsilon) \hat{A}_t) \right]

J^{\theta'}_{TRPO}(\theta) = \mathbb{E}_{(s_t, a_t) \sim \pi_{\theta'}} \left[ \frac{p_{\theta}(a_t|s_t)}{p_{\theta'}(a_t|s_t)} A^{\theta'}(s_t, a_t) \right]， KL(\theta, \theta') < \delta

PPO将KL散度作为惩罚项，而TRPO只计算KL散度较小部分区域.

Q值估计了一个Actor在某个状态后的表现会有多好.

暂时掠过

RLHF会有两阶段的训练: 第一阶段训练出一个奖励模型，用于奖励人类所偏好的答案; 第二阶段根据训练出的模型来后训练模型.

Reward Model

\text{loss}(\theta) = -\frac{1}{\left(\frac{K}{2}\right)} \mathbb{E}_{(x, y_w, y_l) \sim D} \left[ \log \left( \sigma \left(r_{\theta}(x, y_w) - r_{\theta}(x, y_l) \right) \right) \right]

Post-train(最好和原数据一起训练，防止灾难性遗忘)

\begin{aligned} \text{objective}(\phi) = & \; \mathbb{E}_{(x, y) \sim D_{\pi_\phi^{\text{RL}}}} \left[ r_{\theta}(x, y) - \beta \log \left(\pi_\phi^{\text{RL}}(y \mid x) / \pi^{\text{SFT}}(y \mid x)\right) \right] \\ & + \gamma \mathbb{E}_{x \sim D_{\text{pretrain}}} \left[ \log\left( \pi_\phi^{\text{RL}}(x) \right) \right] \end{aligned}

具体原理没看懂，简单来说就是不训练Reward Model了，直接在原模型上SFT.

\mathcal{L}_{\text{DPO}}(\pi_\theta; \pi_{\text{ref}}) = -\mathbb{E}_{(x, y_w, y_l) \sim \mathcal{D}} \left[ \log \sigma \left( \beta \log \frac{\pi_\theta(y_w \mid x)}{\pi_{\text{ref}}(y_w \mid x)} - \beta \log \frac{\pi_\theta(y_l \mid x)}{\pi_{\text{ref}}(y_l \mid x)} \right) \right]

让大模型生成多条回,用这几条回答的平均值作为baseline, 然后和PPO差不多

\mathcal{J}_{\text{GRPO}}(\theta) = \mathbb{E}\Big[q \sim P(Q), \{o_i\}_{i=1}^G \sim \pi_{\theta_{\text{old}}}(O|q)\Big] \\ \frac{1}{G} \sum_{i=1}^G \frac{1}{|o_i|} \sum_{t=1}^{|o_i|} \left\{ \min \left[ \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i,<t})} \hat{A}_{i,t}, \operatorname{clip} \left( \frac{\pi_\theta(o_{i,t}|q,o_{i,<t})}{\pi_{\theta_{\text{old}}}(o_{i,t}|q,o_{i,<t})}, 1-\epsilon,\, 1+\epsilon \right) \hat{A}_{i,t} \right] - \beta \mathbb{D}_{\text{KL}} \left[ \pi_\theta \| \pi_{\text{ref}} \right] \right\}

\hat{A}_{i,t} = \tilde{r}_i = \frac{r_i - \operatorname{mean}(\mathbf{r})}{\operatorname{std}(\mathbf{r})}

\mathbb{D}_{\text{KL}} \left[ \pi_\theta \| \pi_{\text{ref}} \right] = \frac{\pi_{\text{ref}}(o_{i,t}|q,o_{i,<t})}{\pi_\theta(o_{i,t}|q,o_{i,<t})} - \log \frac{\pi_{\text{ref}}(o_{i,t}|q,o_{i,<t})}{\pi_\theta(o_{i,t}|q,o_{i,<t})} - 1